
Responsible: Frederik de Lichtenberg
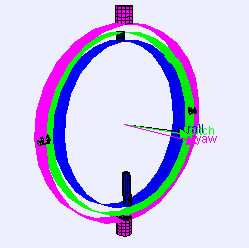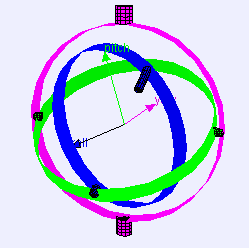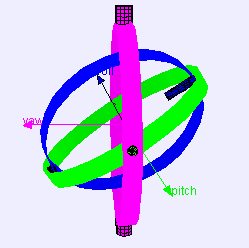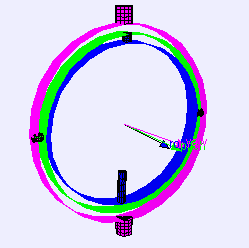
Upon rotating a system of three interlocked gimbals around their respective axes one would lose one degree of freedom when two of the gimbals are driven into a parallell configuration. Up until now, the SACP has been using Euler angles to communicate to it’s gimbal camera system in which direction to move, which means the mounted camera have become a victim to gimbal lock everytime it turned 90 degrees upwards or downwards from its initial position. This is unfortunate as it limits the cameras further movement, due to the software being confused about the cameras positioning. This problem has lead to many complications throughout the years; NASA’s Apollo missions solved the problem with the use of sextants. SACP has partially solved the problem by choosing beforehand if the camera is to be pointed in a horizontal or vertical position, and then limited its further moveability. Both these solutions, however, have luckily become outdated, as a mathematical solution has emerged: Quaternions!
Quaternions are the basis of a four dimensional number system discovered by William Rowan Hamilton in 1843. Quaternions form an interesting algebra where each object contains 4 scalar variables, these objects can be added and multiplied as a single unit in a similar way to the usual algebra of numbers. However, there is a difference, unlike the algebra of scalar numbers qa * qb is not necessarily equal to qb * qa (where qa and qb are quaternions). In mathematical terms, quaternion multiplication is not commutative. Quaternions have 4 dimensions (each quaternion consists of 4 scalar numbers), one real dimension and 3 imaginary dimensions. Each of these imaginary dimensions has a unit value of the square root of -1, but they are different square roots of -1 all mutually perpendicular to each other, known as i,j and k. These special feautres results in quaternions being a brilliant solution when rotating in three degrees, completely avoiding the gimbal lock problem. If you want to read more about quaternions and how they work, you can visit http://www.euclideanspace.com/maths/algebra/realNormedAlgebra/quaternions/index.htm.
Our first milestone is to overcome the gimbal lock problem by implementing a system based on quaternions. This means that we have to rebuild the SACP system from the bottom-up – a very time-consuming project, but none the less a crucial one. When this problem is taken care of, every other project, such as GPS targeting, automated panorama and timelapse will be much easier to implement.
Responsible: Kamilla Bolstad and Alender Fosseidbråten
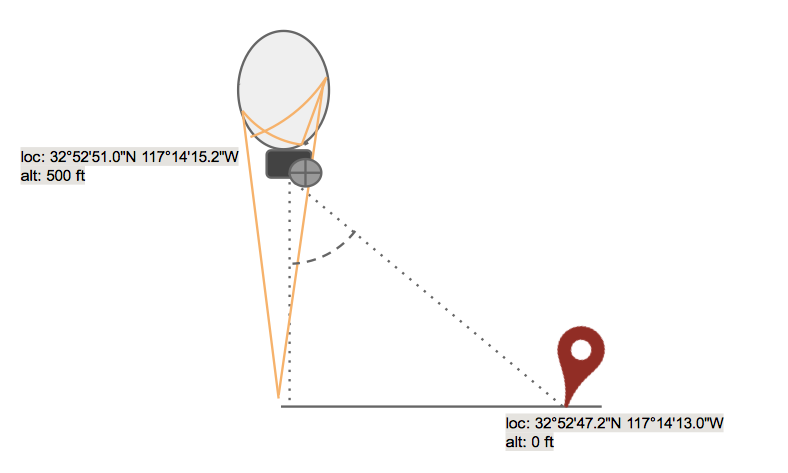
Today, if you want to snap a picture of a certain geographical location, you have to manually steer the camera to face towards the intende point before telling it to take the picture. As with the panorama and timeplapse (M.3) we wish to automate this process. With the use of triangulation we will let the arduino chip calculate the necessary angle and direction of the camera to
capture the GPS-point feeded to it. In the role of the altimeter, we have the Freescale’s MPL115A1 Barometer. We know the pressure at sealevel, and the barometer tells us the pressure around the SACP, and these to factors allows us to calculate the height of the rig. As far as the direction of the camera is concerned, we have CHRobotics’ Intertial Measuring Unit (IMU), CHR-UM6 that lets us know the camera’s direction relative to north at all times. Last, but not least, we can read the SACP GPS location with the use of Ublox’ NEO-6M GPS. Now we have all the needed inputs to equate the direction and angle of the camera!
As a stretch goal we intend to allow the user to feed the SACP with a series of GPS locations and time points. This is so that the SACP can automatically rotate and snap a picture of a single point at a specific time, and then later rotate to the next point on the schedule and snap another picture. We call it “GPS Scheduling”. This would be useful if, say, you deployed the SACP in the middle of Coachella and you wanted it to snap a picture of different stages when specific bands are playing. Set the schedule, deploy the rig, and enjoy the concerts!
Responsible: Thomas Emil Dagsvik
As it is now, the SACP is brilliant for taking great panoramas from the sky. There is only one catch: you have to manually tell the camera to move a couple of inches in one direction, snap a picture, and repeat until you have covered the area you wish photograph. Seeing as this is harder than it needs to be, we intend to create an automated panorama system, that turns and snaps pictures on its own. Hello future!
A timelapse is a series of pictures of a fixed target taken over a longer time period with short intervals, as can be seen in the video below. When SACP created the timelapse of the Native Diver Excavation, they manually took a picture every 30 seconds for the entirety of the project. Upon cutting the movie, they needed to use advanced computer vision to stabilize the picture around the target, as can be observed in the video as the black boxes in the corners. Both these methods are unecessary, time-consuming and boring. Not only do we intend to create an automated timelapse system that snaps picture on its own, we also hope to use our the GPS tracking system to automatically stabilize and center the camera towards the intended target.